[연재] 코틀린 프로그래밍 - 연산자
Note:이 글은 'Do it! Kotlin Programming'의 일부의 내용을 연재하고 있습니다. 완전한 내용은 책을 참고 하세요!
코틀린 연산자
이번 글에서는 다른 언어에서 사용하는 연산자와 함께 코틀린에만 있는 연산자와 코틀린에서 사용하지 않는 연산자에 대해 이야기합니다. 예를 들어 자바의 삼항 연산자는 코틀린에서 사용하지 않습니다. 또 단항, 이항 등과 같은 연산자 용어와 연산자의 우선순위를 알아두는 것도 중요합니다. 그러니 연산자를 공부한 적이 있어도 다시 한 번 공부하는 것을 추천합니다. 지금부터 코틀린에서 사용되는 연산자를 하나씩 공부해 보겠습니다.
기본 연산자
코틀린의 기본 연산자는 산술, 대입, 증가, 감소, 비교, 논리 연산자 등의 종류가 있습니다. 그러면 먼저 수식의 구조부터 시작해서 각각의 연산자를 하나씩 알아보겠습니다.
수식의 구조 이해하기
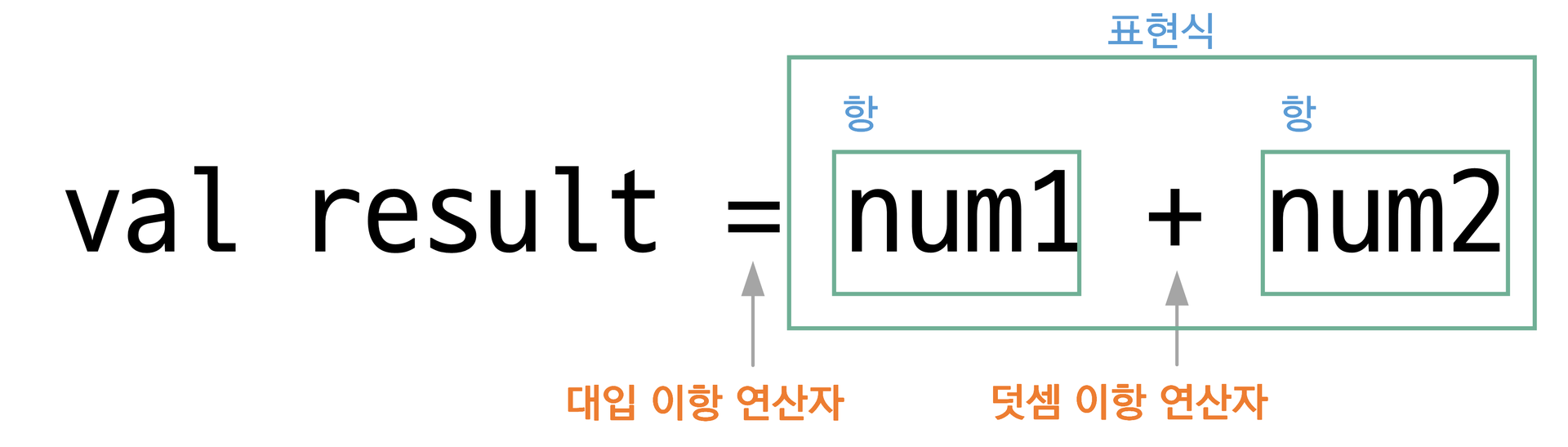
다음은 코틀린으로 작성한 수식입니다. 연산자를 공부하기 전에 수식의 구조에 대해 간단히 알아보겠습니다. 수식에 있는 더하기는 산술 연산자이고 num1, num2와 같이 연산에 사용되는 값은 항입니다. 이때 연산자는 항의 개수에 따라서 단항 연산자(항이 1개), 이항 연산자(항이 2개), 삼항 연산자(항이 3개)로 구분합니다. 다음은 이항 연산자인 덧셈을 사용하여 작성한 수식입니다.
산술 연산자
사칙연산에 사용되는 사칙 연산자(+, -, *, /)와 나머지 연산자(%)를 산술 연산자라 부릅니다. 다음은 산술 연산자와 산술 연산자의 사용 예를 표로 정리한 것입니다.
| 연산자 | 의미 | 사용 예 |
|---|---|---|
| + | 덧셈 | 3 + 2 |
| - | 뺄셈 | 3 - 2 |
| * | 곱셈 | 3 * 2 |
| / | 나눗셈 | 3 / 2 |
| % | 나머지(Modulus) | 3 % 2 |
사칙연산은 사용 예만 읽어봐도 금방 알 수 있죠? 그러면 나머지 연산에 대해서만 설명해 보겠습니다. 나머지 연산은 2번째 항으로 1번째 항을 나눈 나머지를 반환합니다. 예를 들어 3%2의 결괏값은 1입니다. 나머지 연산은 홀수나 짝수 같은 특정 구간의 수를 알아낼 때 유용합니다. 다음은 홀수와 짝수를 검사하는 코드입니다. 어떤 숫자(n)를 2로 나누었을 때 나머지가 1이면 홀수, 0이면 짝수인 것을 이용한 것이죠.
Tip:10으로 나눈 나머지를 이용하면 어떤 수의 1의 자리 수만 얻을 수도 있습니다.
...
if ((n % 2) == 1) { // 홀수
println("n is an Odd number")
}
if ((n % 2) == 0) { // 짝수
println("n is an Even number")
...
대입 연산자
대입 연산자(=)는 변수에 값을 할당하는 연산자입니다. 그리고 대입 연산자는 이항 연산자 중 우선 순위가 가장 낮습니다. 쉽게 말해 다른 연산자의 연산이 모두 끝나면 그때 대입 연산자가 동작합니다. 대입 연산자 오른쪽에는 값이나 값이 있는 변수, 표현식 등이 사용됩니다. 다음은 대입 연산자를 활용한 예입니다. 지금까지 공부한 내용으로 대입 연산자는 자연스럽게 이해하고 있을 것입니다.
val numOfApple = 12 // 변수가 대입 연산자에 의해 할당
val result = numOfApple - 2 // 표현식이 대입 연산자에 의해 결괏값 할당어떤 변수에 저장된 값(num)으로 연산을 수행한 다음 그 결괏값(num + 2)을 다시 변수(num)에 할당할 때 산술 연산자와 대입 연산자를 함께 사용하여 간결하게 표현할 수도 있습니다.
num = num + 2 // 산술 연산자와 대입 연산자를 함께 사용하는 경우
num += 2 // 이렇게 간략하게 표현1번째 코드와 2번째 코드의 실행 결과는 같지만 실무에서는 간결하게 표현한 2번째 방법을 더 선호합니다. 다음은 대입 연산자를 모두 정리한 표입니다.
대입 연산자
| 연산자 | 의미 | 사용예 |
|---|---|---|
| = | num = 2 | |
| += | 두 항을 더한 후 왼쪽 항에 대입 | num += 2 |
| -= | 왼쪽 항을 오른쪽 항으로 뺀 후 왼쪽 항에 대입 | num -= 2 |
| *= | 두 항을 곱한 후 왼쪽 항에 대입 | num *= 2 |
| /= | 왼쪽 항을 오른쪽 항으로 나눈 후 왼쪽 항에 대입 | num /= 2 |
| %= | 왼쪽 항을 오른쪽 항으로 나머지 연산 후 왼쪽 항에 대입 | num %= 2 |
증가 연산자와 감소 연산자
증가 연산자와 감소 연산자는 항이 1개인 단항 연산자입니다. 증가, 감소 연산자는 항의 앞이나 뒤에 붙여 사용하며 이름 그대로 1을 더하거나 빼는 연산을 수행합니다. 다음은 증가, 감소 연산자를 정리한 표입니다.
| 연산자 | 의미 | 사용 예 |
|---|---|---|
| ++ | 항의 값에 1 증가 | ++num 또는 num++ |
| -- | 항의 값에 1 감소 | --num 또는 num-- |
단, 증가, 감소 연산자는 항 앞에 붙이는 경우와 뒤에 붙이는 경우 연산 결과가 다르므로 주의해야 합니다. 항 앞에 증가, 감소 연산자를 붙이면 연산을 마친 다음 그 값을 대입합니다. 하지만 항 뒤에 증가, 감소 연산자를 붙이면 먼저 그 값을 대입한 다음 연산을 수행합니다.
| 증가, 감소 연산자 사용하기 | IncDecOperator.kt |
package chap02.section4
fun main() {
var num1 = 10
var num2 = 10
val result1 = ++num1 // num 값 증가 후 대입
val result2 = num2++ // 먼저 num 값 대입 후 증가
println("result1: $result1")
println("result2: $result2")
println("num1: $num1")
println("num2: $num2")
}
| Result |
result1: 11 result2: 10 num1: 11 num2: 11
증가 연산자를 앞에 사용하는 num1의 경우에는 num1 값을 증가한 후 대입하고 증가 연산자를 뒤에 사용한 num2의 경우에는 먼저 값을 대입한 후 증가합니다. 따라서 result1은 11이지만 result2는 10이 할당됩니다. 최종 결과인 num1, num2를 출력하면 결과는 동일한 11을 출력합니다. 이것은 감소 연산자(--)에도 그대로 적용됩니다.
비교 연산자
비교 연산자는 두 개의 항을 비교하기 위해 사용합니다. 모든 비교 연산자는 비교 결과가 참이면 true를, 거짓이면 false를 반환합니다. 다음은 비교 연산자를 표로 정리한 것입니다. 대부분의 비교 연산자는 기초 수학 수준의 지식만 있으면 바로 이해할 수 있습니다.
비교 연산자
| 연산자 | 의미 | 사용 예 |
|---|---|---|
| > | 왼쪽이 크면 true, 작으면 false 반환 | num > 2 |
| < | 왼쪽이 작으면 true, 크면 false 반환 | num < 2 |
| >= | 왼쪽이 크거나 같으면 true, 아니면 false | num >= 2 |
| <= | 왼쪽이 작거나 같으면 true, 아니면 false | num <= 2 |
| == | 두 개 항의 값이 같으면 true, 아니면 false | num1 == num2 |
| != | 두 개 항의 값이 다르면 true, 아니면 false | num1 != num2 |
| === | 두 개 항의 참조가 같으면 true, 아니면 false | num1 === num2 |
| !== | 두 개 항의 참조가 다르면 true, 아니면 false | num1 !== num2 |
삼중 등호와 부정 이중 등호 연산인 참조(===, !==) 연산자는 자바에는 없지만 코틀린에는 존재하는 연산자입니다. === 연산자는 왼쪽과 오른쪽 항의 참조 주소가 같은지 검사하며 참조 주소가 같으면 true, 다르면 false를 반환하고, !==의 경우는 반대로 참조 주소가 다르면 true를 반환하고 아니면 false를 반환 합니다.
논리 연산자
논리 연산자에는 논리곱 연산자, 논리합 연산자, 부정 연산자가 있습니다. 논리곱 연산자(&&)는 2개의 항이 모두 true인 경우에만 true를 반환하고 논리합 연산자(||)는 2개의 항 중에 1개의 항만 true이면 true를 반환합니다. 부정 연산자(!)는 true과 false의 값을 반대로 바꿉니다. 다음은 논리 연산자를 정리한 표입니다.
| 연산자 | 의미 | 사용예 |
|---|---|---|
| && | 논리곱으로 두 항이 모두 true일 때 true, 아니면 false | exp1 && exp2 |
| || | 논리합으로 두 항 중 하나의 항이 true일 때 true, 아니면 false | exp1 || exp2 |
| ! | 부정 단항 연산자로 true를 false로, false를 true로 바꿈 | !exp |
논리 연산자는 비교 연산자와 함께 사용하는 경우가 많습니다. 예를 들어 (5 > 3) && (5 > 2)는 (5 > 3), (5 > 2) 순서로 비교 연산자를 실행하여 두개의 항이 모두 true이므로 true && true 형태로 논리곱 연산이 평가되어 최종적으로 true를 반환합니다. 그런데 논리 연산자를 사용할 때 주의해야 할 점이 하나 있습니다. 다음 코드를 볼까요?
var check = (5>3) && (5>2) // 2개의 항((5>3), (5>2))이 모두 참이면 true
check = (5>3) || (2>5) // 2개 중 1개의 항이 참이면 true
check = !(5>3) // true는 false로, false는 true로 변경위의 코드에서 논리합(||) 연산자의 경우 왼쪽의 항이 true이면 코틀린 컴파일러는 오른쪽 항을 아예 평가(실행)하지 않습니다. 어차피 논리합 연산자는 왼쪽이나 오른쪽의 항 중 1개의 항만 true이면 true를 반환하기 때문이죠. 이것을 단축 평가(Short Circuit Evaluation)라고 부릅니다.
Tip:논리곱 연산자도 마찬가지 입니다. 왼쪽 항이 false라면 오른쪽 항을 평가하지 않고 바로 false를 반환합니다.
비트 연산자
비트(bit) 연산자는 기계가 이해할 수 있는 값인 0과 1을 처리하는 데 사용합니다. 비트 연산자는 프로그래머가 기기를 직접 제어해야 하는 경우 아주 유용하게 사용됩니다. 보통 IoT 기기를 위한 컨트롤러를 접근하거나 프로세서의 레지스터에 접근하는 임베디드 시스템 프로그래밍(Embeded System Programming) 분야에서 비트 연산을 많이 하죠.
비트와 비트 연산 이해하기
비트 연산자를 공부하려면 변수에 저장되는 값을 비트로 표현할 수 있어야 합니다. 다음은 Int형 값 10을 비트로 표현한 것입니다. 이때 10을 비트로 표현하는 방법은 아주 간단합니다. 10을 2진수로 바꾸면 됩니다.
▶ 1010(2) = 21+23 = 10(10)
▶ 가장 왼쪽에 있는 비트는 양(+), 음(-)을 판단하는 데 사용합니다.
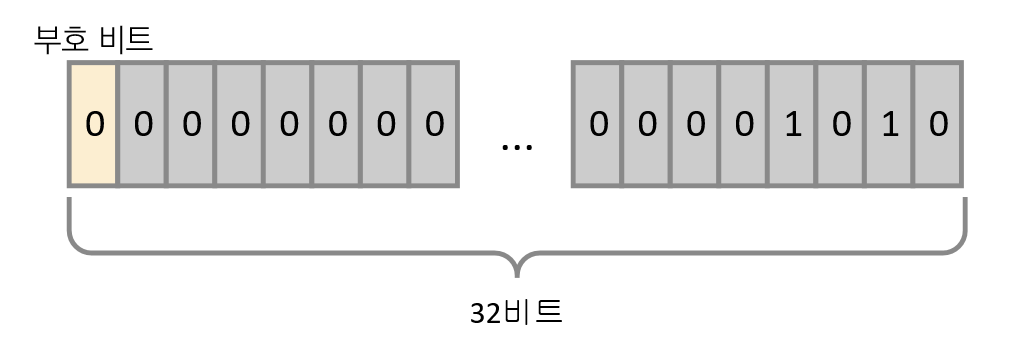
10이 비트로 어떻게 표현되는지 알았으니 비트 연산이 어떤 것인지 간단하게 알아보겠습니다. 다음은 32비트 컴퓨터에 1을 저장한 상태를 비트로 나타낸 것입니다.
0000 0000 0000 0000 0000 0000 0000 0001
비트 연산 중에는 비트를 왼쪽으로 밀어내는 연산이 있습니다. 이 상태에서 비트를 왼쪽으로 2만큼 밀어내면 어떻게 될까요? 그러면 다음과 같은 상태가 됩니다. 비트는 2만큼 밀었지만 실제 값은 1에서 4로 바뀝니다.
0000 0000 0000 0000 0000 0000 0000 0100
만일, 위의 상태에서 비트를 끝까지(31비트) 밀어내면 어떻게 될까요? 부호 비트에 1이 들어가고 나머지 비트가 모두 0이 됩니다. 이 경우 실제 값은 4에서 -2,147,483,648로 바뀝니다.
▶ 음수로 표현할 수 있는 최댓값은 비트로 1000…0000으로 표현합니다.
1000 0000 0000 0000 0000 0000 0000 0000
또, 비트 연산 중에는 모든 비트를 뒤집는 연산도 있습니다. 예를 들어 위의 값을 뒤집으면 0111…1111이 됩니다. 부호 비트는 0이므로 양수이고 나머지 비트는 모두 1이므로 32비트로 표현할 수 있는 양수 중 최댓값이라고 생각할 수 있습니다. 즉, 2,147,483,647를 손쉽게 구할 수 있습니다.
0111 1111 1111 1111 1111 1111 1111 1111
비트 연산을 위한 비트 메서드
비트 연산이 무엇인지 이해했나요? 그러면 본격적으로 비트 연산을 위한 메서드를 모두 알아보겠습니다. 이런 메서드들은 메서드처럼 사용해도 되지만 연산자처럼 사용할 수도 있습니다. 예를 들어 비트 전체를 왼쪽으로 이동시키는 shl 메서드는 4.shl(1) 또는 4 shl 1과 같은 방법으로 사용할 수 있습니다.
▶ 4 shl 1과 같이 멤버에 접근하는 점(.) 연산자와 소괄호를 생략하는 표현식을 중위 표현식이라고 부릅니다.
다음은 비트 연산자(메서드)를 정리한 표입니다. 아직 비트 연산자를 제대로 공부하지는 않았지만 표를 통해 어떤 비트 연산자가 있는지 읽어보고 넘어가기를 권합니다.
비트 연산자
| 표현식 | 설명 |
|---|---|
| 4.shl(bits) | 4를 표현하는 비트를 bits만큼 왼쪽으로 이동(부호 있음) |
| 7.shr(bits) | 7을 표현하는 비트를 bits만큼 오른쪽으로 이동(부호 있음) |
| 12.ushr(bits) | 12를 표현하는 비트를 bits만큼 오른쪽 이동(부호 없음) |
| 9.and(bits) | 9를 표현하는 비트와 bits를 표현하는 비트로 논리곱 연산 |
| 4.or(bits) | 4를 표현하는 비트와 bits를 표현하는 비트로 논리합 연산 |
| 24.xor(bits) | 23를 표현하는 비트와 bits를 표현하는 비트의 배타적 연산 |
| 78.inv | 78을 표현하는 비트를 모두 뒤집음 |
비트 이동 연산자 shl, shr 이해하기
비트 이동 연산자에는 shl, shr이 있습니다. 각 연산자는 비트를 왼쪽(left)이나 오른쪽(right)으로 밀어낸 다음 사라진 비트의 값은 0으로 채우며 부호 비트는 그대로 둡니다. 설명이 조금 어렵죠? 다음 예시를 살펴보면 금방 이해될 것입니다. 다음은 14(10)의 비트를 오른쪽으로 1칸 밀어낸 것입니다.
0000 00(생략).. 1110 -> 23 + 22 + 21 = 8 + 4 + 2 = 14 0000 00(생략).. 0111 -> 22 + 21 + 20 = 4 + 2 + 1 = 7
가장 왼쪽의 비트가 1 이므로 음수입니다. 그런데 비트를 오른쪽으로 1칸밀었더니 2번째 자리는 0으로 채워지고 부호 비트는 그대로 남았습니다. 즉, 14에서 7로 변했습니다. 비트 이동 연산자 shl, shr은 부호 비트는 이동시키지 않으면서 사라진 비트의 값을 0으로 채운다는 말이 잘 이해되었나요?
그런데 비트 이동 연산자는 왜 사용할까요? 비트 이동 연산자는 컴퓨터가 쉽게 다룰 수 있는 비트를 이용하여 연산하는 것이기 때문에 연산 속도가 아주 빠르다는 장점이 있습니다. 예를 들어 4에 2를 곱하는 것보다 비트 이동 연산자를 이용하여 비트를 왼쪽으로 1칸 밀어내는 것이 더 빠릅니다. 이때 비트를 왼쪽으로 1칸 밀어내는 것을 2를 곱하는 것으로, 비트를 오른쪽으로 1칸 밀어내는 것을 2로 나눈다고 생각하면 비트 이동 연산자를 이해할 때 도움이 될 것입니다.
4 shl 1 -> 비트를 왼쪽으로 1칸 옮기는 것은 2를 곱하는 것과 같음 0000 ..(생략).. 0100 -> 4 0000 ..(생략).. 1000 -> 4의 비트를 왼쪽으로 1칸 옮기면? 8
비트를 왼쪽으로 밀어내는 것이 어떤 의미를 가지고 있는지 완벽하게 이해해 보세요.
5 shl 1 의 예 -> 5의 비트를 왼쪽으로 1칸 옮김 0000 0101 -> 22 + 20 = 5 0000 1010 -> 23 + 21 = 10 (5 x 2의 결과와 동일) 5 shl 2 의 예 -> 5의 비트를 왼쪽으로 2칸 옮김 0000 0101 -> 22 + 20 = 5 0001 0100 -> 24 + 22 = 16 + 4 = 20 (5 x 4의 결과와 동일)
다음은 코드에서 shl을 활용한 예입니다.
// 코드의 예
println(4 * 2)
println(4.shl(1)) // 멤버 메서드 접근 방식으로 표현
println(4 shl 1) // shl에 중위 표현법으로 사용
다음은 오른쪽으로 비트를 1칸 밀어낸 예와 코드로 shr을 활용한 예입니다.
64 shr 2의 예 -> 64의 비트를 오른쪽으로 2칸 옮김 0100 0000 -> 26 = 64 0001 0000 -> 24 = 16 (64에 4를 나눈값과 동일)
println(64 / 4)
println(64 shr 2)단, 아주 큰 값에 비트 이동 연산자를 사용할 때는 부호 비트에 주의해야 합니다. 만약 비트 부호가 바뀌면 예상하지 못한 결과를 얻을 수 있기 때문입니다. 그러면 다음 예제를 통해 비트 이동 연산자를 마무리하겠습니다.
| 비트 이동 연산자 사용하기 | BitsShift.kt |
package chap02.section4
fun main() {
var x = 4
var y = 0b0000_1010 // 10진수 10
var z = 0x0F // 10진수 15
println("x shl 2 -> ${x shl 2}") // 16
println("x.inv -> ${x.inv}") // -5
println("y shr 2 -> ${y/4}, ${y shr 2}") // 2, 2
println("x shl 4 -> ${x*16}, ${x shl 4}") // 64, 64
println("z shl 4 -> ${z*16}, ${z shl 4}") // 240, 240
x = 64
println("x shr 4 -> ${x/4}, ${x shr 2}") // 16, 16
}
| Result |
x shl 2 -> 16 x.inv -> -5 y shr 2 -> 2, 2 x shl 4 -> 64, 64 z shl 4 -> 240, 240 x shr 4 -> 16, 16
지금까지는 여러분의 이해를 돕기 위해 변수에 저장된 값을 10진수로 가정했습니다. 하지만 2진법, 16진법에도 비트 이동 연산자를 사용할 수 있습니다. 특히 16진법은 1자리의 숫자가 2진법의 4자리 숫자를 표현하기 때문에 실무에서 많이 이용합니다.
▶ 예를 들어 16진수 F는 2진수 1111이므로 FF는 1111 1111로 이해합니다.
비트 이동 연산자 ushr 이해하기
비트 연산자 ushr을 이용하면 제일 왼쪽 비트에 0을 밀어 넣으면서 오른쪽으로 비트가 이동합니다. 즉, 부호 비트까지 포함하여 비트를 밀어냅니다. 이런 특징 때문에 음수인 경우 주의해서 사용해야 합니다. 부호 비트가 1에서 0으로 바뀌기 때문이죠. 다음 코드를 통해 shr와 ushr에 어떤 차이가 있는지 알아보겠습니다.
| ushr 이해하기 | UshrEx.kt |
package chap02.section4
fun main() {
val number1 = 5
val number2 = -5
println(number1 shr 1)
println(number1 ushr 1) // 변화 없음
println(number2 shr 1) // 부호 비트가 1로 유지
println(number2 ushr 1) // 부호 비트가 0이 되면서 변경
}
| Result |
2 2 -3 2147483645
4번째 실행 결과를 보면 엄청나게 큰 값이 출력되어 있습니다. 왜 이런 결과가 나왔는지 생각해 보겠습니다. -5는 다음과 같이 표현합니다.
▶ 음수는 2의 보수로 표현합니다.
1111 11(생략)11 1111 1011 -> -5
다음은 -5 ushr 1의 결과입니다. ushr을 사용할 때는 음수가 2의 보수로 표현된다는 점에 주의해야 합니다.
0111 11(생략)11 1111 1101 -> 부호 비트가 0으로 바뀌며 0111 11(생략)11 1111 1101의 값인 2,147,483,645가 됨
논리합 연산자 or 이해하기
이제 논리합 연산자 or에 대해 알아보겠습니다. or는 두 수의 비트를 일대일 대응으로 비교하며 비트의 값이 하나라도 1이면 1을 반환합니다. 설명이 조금 어렵죠? 다음 예시와 함께 or 연산자에 대해 알아보겠습니다.
12 = 0000 1100 (이진 값) OR 25 = 0001 1001 (이진 값) --------------------- 29 = 0001 1101 (이진 값)
12는 0000 1100으로, 25는 0001 1001로 표현할 수 있습니다. 이때 12 or 25의 결괏값은 12와 25의 비트를 하나씩 대응하며 논리합 연산을 합니다. 예를 들어 12의 첫 번째 자리 비트인 0과 25의 첫 번째 자리 비트인 1로 or 연산을 하여 1을 반환합니다. 두 번째 자리도 마찬가지입니다. 0과 0으로 or 연산한 결과인 0을 반환합니다. 최종 결괏값은 0001 1101, 즉, 29가 나옵니다. 다음은 위의 예시를 코드로 입력한 것입니다. 프로그램을 실행하여 논리합 연산을 마무리해 보세요.
| 비트 논리 연산자 테스트하기 | LogicalBitwise.kt |
package chap02.section4
fun main() {
val number1 = 12
val number2 = 25
val result: Int
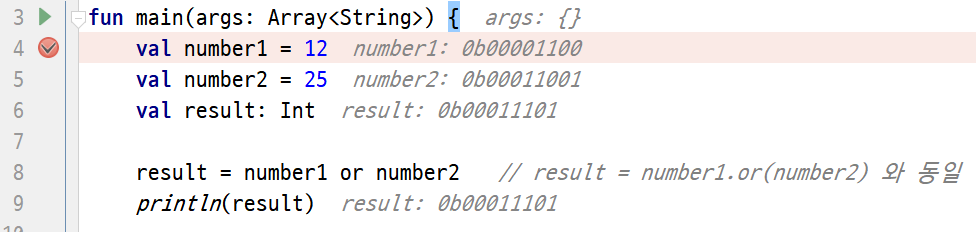
result = number1 or number2 // result = number1.or(number2)와 동일
println(result)
}
| Result |
29
디버깅 도구로 비트 연산 과정 살펴보기
지금까지는 비트를 여러분이 직접 상상해야 했습니다. 하지만 디버깅 도구를 이용하면 비트의 변화를 쉽게 살펴볼 수 있습니다. LogicalBitwise.kt 파일을 그대로 두고 다음 내용을 따라해 보세요.
1. val number1 = 12 가 입력된 곳으로 이동하세요. 그런 다음 줄 번호 오른쪽의 빈 공간(회색 부분)을 누르세요. 그러면 빨간색 점으로 브레이크포인트(Breakpoint)가 생성됩니다. 단축키로 브레이크포인트를 생성하려면 원하는 줄을 마우스로 누른 다음 Ctrl + F8을 누르세요.
▶ MacOS에서는 Cmd+ F8을 누르세요.

2. 그런 다음 [Run > Debug] 메뉴를 선택하세요. 그러면 디버그 모드로 프로그램이 실행됩니다. 과정 1에서 지정했던 브레이크 포인트에서 실행이 멈춥니다.
▶ 윈도우에서는 Shift + F9, MacOS는 Ctrl + D를 눌러도 됩니다.

3. [Run > Step Over] 메뉴를 선택하거나 F8 을 누르면 프로그램이 한 줄씩 실행됩니다. 이때 코드 오른쪽에는 회색으로 현재 변수의 상태가 나타납니다.

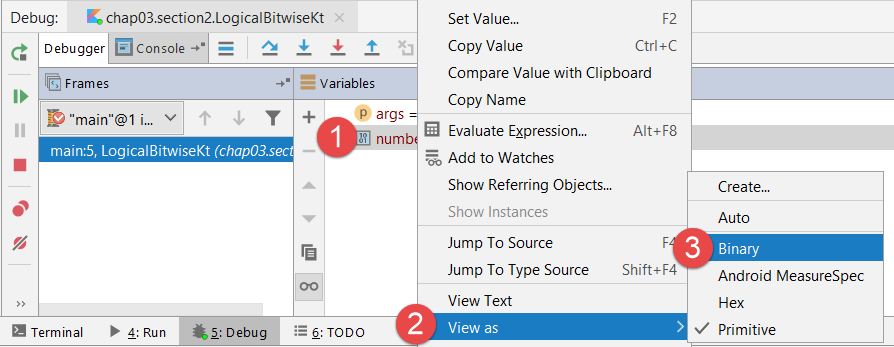
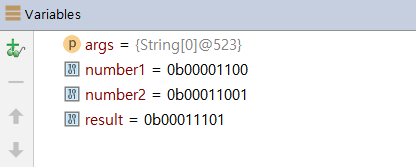
4. 아래쪽에 나타난 디버그 창으로 눈을 돌려보겠습니다. 디버그 창에서 Variables 창을 찾아보세요. 그런 다음 검사하고 싶은 변수 위에 마우스 포인터를 놓고 마우스 오른쪽 버튼을 누르면 메뉴가 나타납니다. [View As > Binary]를 선택하세요. 그러면 Variables 창과 과정 3에서 확인했던 현재 변수의 상태가 이진수로 바뀝니다. 이진수는 곧 비트의 상태이므로 비트의 변화를 쉽게 확인할 수 있겠죠?
▶ 비트 변화에 나타나는 0b는 이진수라는 뜻입니다.
논리곱 연산자 and 이해하기
논리곱 연산자 and는 비트의 값이 둘 다 1이면 1을 반환합니다. 그 이외의 경우는 모두 0을 반환합니다. 다음 예시로 and 연산자를 이해해 보세요. or를 이해했다면 금방 이해할 수 있을 것입니다.
12 = 00001100(2) AND 25 = 00011001(2) --------------------- 8 = 00001000(2)
배타적합 연산자 xor 이해하기
배타적합 연산자 xor는 두 비트 값을 비교하여 같으면 0을, 다르면 1을 반환합니다. or 연산자와 반대의 기능을 한다고 이해하면 됩니다. 다음 예시로 xor 연산자를 이해해 보세요.
1 xor 1 = 0 1 xor 0 = 1 0 xor 1 = 1 0 xor 0 = 0 12 = 00001100 (2) XOR 25 = 00011001 (2) --------------------- 21 = 00010101 (2)
이때 xor의 독특한 성질을 이용하여 두 개의 변수 값을 바꿀 수도 있습니다. 이런 기법을 스왑(swap) 기법이라고 부릅니다. 다음 예제를 작성해 봅시다.
| xor 연산자로 두 값을 스왑하기 | XorSwapTest.kt |
package chap02.section4
fun main() {
var number1 = 12
var number2 = 25
number1 = number1 xor number2
number2 = number1 xor number2
number1 = number1 xor number2
println("number1 = " + number1)
println("number2 = " + number2)
}
| Result |
number1 = 25 number2 = 12
xor 연산자를 세 번 사용하여 두 수를 서로 바꾸었습니다. xor을 이용한 스왑 기법을 사용하면 임시 변수를 놓고 변수를 저장하여 옮기는 등의 작업을 하지 않아도 간편하게 두 수를 바꿀 수 있어 편리합니다.
반전 연산자 inv 이해하기
이제 마지막 비트 연산자입니다. 반전 연산자 inv는 비트를 모두 반대로 뒤집습니다. 이 연산자는 단항 연산자이므로 중위 표현법을 사용하지 않고 메서드처럼 사용합니다. 다음 예시를 통해 반전 연산자를 이해해 보세요.
12 = 0...00001100 (2) 반전 inv --------------------- -13 = 1...11110011 (2) (32bits)

Language
Get in touch with us
"If you would thoroughly know anything, teach it to other."
- Tryon Edwards -



